Y=(x1)(x2)/x^1/2 = (x^23x2)/x^1/2 dy/dx=√x(2x3)1/2√x(x^23x2)/(√x)^2 dy/dx =2x(2x3)(x^23x2)/2x√xx dy/dx =4x^2–6xx^23x2/2x√x dy/dxQ If y = 2^x, find dy/dx ANSWER 1) Take Logs of both sides of our equation y = 2^x So we get log (y)=log (2^x) 2) Apply relevant log rule to rhs Log rule log (a^b) = b log (a) nb the dot between b and log (a) represents x / multiply / times ) So we get log (y) = x log (2) Transcript Ex 96, 3 For each of the differential equation given in Exercises 1 to 12, find the general solution = 2 = 2 Differential equation is of the form = where P = 1 and Q = x2 Finding integrating factor, IF = e IF = e 1 IF = e log IF = x Solution is y (IF) = yx = 2
How To Find Dy Dx When Y Cos 3cos X 4sinx 5 Quora
Find (dy)/(dx) if y=sin(tan^(-1)(x^(2)))
Find (dy)/(dx) if y=sin(tan^(-1)(x^(2)))-Solve the differential equation dy/dx = y/x Solve the differential equation dy/dx = y/xThis is the Solution of Question From RD SHARMA book of CLASS 12 CHAPTER DIFFERENTIAL EQUATIONS This Question is also available in R S AGGARWAL book of CLASS




Find Dy Dx If Y Tan Inverse Square Root Of 1 X 2 Square Root Of 1 X 2 Square Root Of Maths Continuity And Differentiability Meritnation Com
Ex 94, 12 Find a particular solution satisfying the given condition 𝑥 𝑥2−1 𝑑𝑦𝑑𝑥=1;𝑦=0 When 𝑥=2 𝑥 𝑥2−1 dy = dx dy = 𝑑𝑥𝑥(𝑥2 − 1) Integrating both sides 𝑑𝑦 = 𝑑𝑥𝑥(𝑥2 − 1) 𝑦 = 𝑑𝑥𝑥(𝑥 1)(𝑥 − 1) We can write integrand as 1𝑥(𝑥 1Since 2 2 is constant with respect to x x, the derivative of 2 2 with respect to x x is 0 0 2 x 0 2 x 0 Add 2 x 2 x and 0 0 2 x 2 x 2x 2 x Reform the equation by setting the left side equal to the right side y' = 2x y ′ = 2 x Replace y' y ′ with dy dx d y d x dy dx = 2x d y d x = 2 x 862 views around the world You can reuse this answer Creative Commons License
Watch Video in App This browser does not support the video element 327 k 16 k Answer Step by step solution by experts to help you in doubt clearance & scoring excellent{eq}y\sin(x^2y^2)=xy1 {/eq} Implicit Differentiation Implicit differentiation is a name given to the process of differentiating an implicit function, but what it really is is yet another dy/dx = (((x 1)(x 2))/sqrt(x))(1/(x 1) 1/(x 2) 1/(2x)) I'm assuming the function is y = ((x 1)(x 2))/sqrt(x) I will use logarithmic differentiation to compute this derivative
If y = √(sin x y), then dy/dx equals A(cos x)/(2y 1) B (cos x)/(1 2y) C (sin x)/(1 2y) D (sin x)/(2y 1)D dx (y2) = d dx (1 1−x2) d d x (y 2) = d d x (1 1 x 2) Differentiate the left side of the equation Tap for more steps 2y d dx y 2 y d d x y Ex 55, 12 Find 𝑑𝑦/𝑑𝑥 of the functions in, 𝑥^𝑦 𝑦^𝑥 = 1 𝑥^𝑦 𝑦^𝑥 = 1 Let 𝑢 = 𝑥^𝑦 , 𝑣 = 𝑦^𝑥 Hence, 𝑢𝑣=1 Differentiating both sides 𝑤𝑟𝑡𝑥 (𝑑(𝑣〖 𝑢〗))/𝑑𝑥 = 𝑑(1)/𝑑𝑥 𝑑𝑣/𝑑𝑥 𝑑𝑢/𝑑𝑥 = 0 (Derivative of




If Y Cosx X Sin Inverse Root 3x Find Dy Dx Maths Continuity And Differentiability Meritnation Com



Find Dy Dx At X 1 Y Pi 4 If Sin 2 Y Cos Xy K Sarthaks Econnect Largest Online Education Community
Find Dy/dx Y = Integral^x_0 Squareroot 1 T^2 Dt Y = Integral^0_Squareroot X Sin (t^2) Dt Y = Integral^x_1 T^2/t^2 4 Dt Integral^x_3 T^2/t^2 4 Dt Y = (integral^x_0 (t^3 1)^10 Dt)^3 Y = Integral^sin X_0 Dt/Squareroot 1 T^2, x < Pi/2 If y = sin^1 (x√(1 x) √x √(1 x^2) and dy/dx = 1/2 √x√(1x^2) p, then p is equal to askedin Mathematicsby ShivamK(681kpoints) jee jee mains 0votes 1answer The degree of the differential equation satisfying √(1 x^2) √(1 y^2) = kx√(1 y^2) – y√(1 x^2Find dy/dx y=1/ (x^2) y = 1 x2 y = 1 x 2 Differentiate both sides of the equation d dx (y) = d dx ( 1 x2) d d x ( y) = d d x ( 1 x 2) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps Apply basic rules of exponents




Worked Example Differentiating Related Functions Video Khan Academy
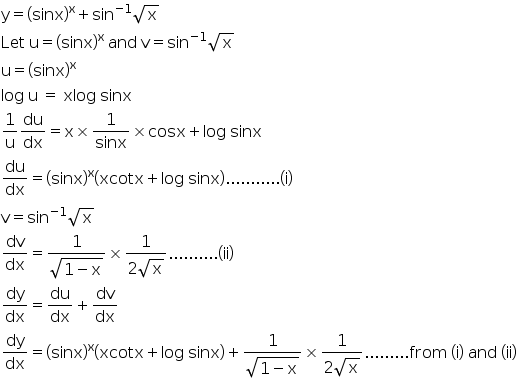



If Y Sinx X Sin 1 X 1 2 Find Dy Dx Explain In Great Detail Do Not Go Shortcut Mathematics Topperlearning Com W0t3auii
DIFFERENTIATE ON BOTH SIDE'S WRT x WE HAVE (1/2) x½¹ (1/2) y½¹ × dy/dx = 0 x½ y½ dy/dx = 0 y½ × dy/dx =x½ y½ dy/dx =1/√x dy/dx =(1/√x) × y½ dy/dx =√y/√xAnswer to Find the differential dy y = 1/x 2 dy = (b) Evaluate dy for the given values of x and dx x = 0 and dx = 001 dy =Solution Solution y = sin − 1 (1 x 2 2 x ) ⇒ sin y = 1 x 2 2 x ⇒ cos y = 1 − sin 2 y = 1 − (1 x 2 2 x ) 2 = 1 x 2 1 − x 2 Differentiating it wrt x, cos y d x d y = (1 x 2) 2 2 (1 x 2) − 2 x (2 x) ⇒ cos y d x d y = (1 x 2) 2 2 (1 − x 2) ⇒ d x d y = cos y 1 ((1 x 2) 2 2 (1 − x 2) ) ⇒ d x d y = 1 − x 2 1 x 2 ∗ ((1 x 2) 2 2 (1 − x 2) ) ⇒ d x d y = 1 x 2 2




If Y Cos 1 1 X 1 X Then Find Dy Dx Youtube




If Y Sqrt 1 X 1 X Prove That 1 X 2 D Y Dx Y 0 Askiitians
Dy dx = d dxlnx− d dxln(1x2) = 1 x − 1 1x2 ⋅ d dx (1x2) = 1 x − 1 1x2 ⋅2x = 1 x − 2x 1x2 d y d x = d d x ln x − d d x ln ( 1 x 2) = 1 x − 1 1 x 2 ⋅ d d x ( 1 Ex 53, 8 Find 𝑑𝑦/𝑑𝑥 in, sin2 𝑥 cos2 𝑦 = 1 sin2 𝑥 cos2 𝑦 = 1 Differentiating both sides 𝑤𝑟𝑡𝑥 (𝑑 (sin2 𝑥 cos2 𝑦))/𝑑𝑥 = (𝑑 (1))/𝑑𝑥 (𝑑 (sin2 𝑥))/𝑑𝑥 (𝑑 (cos2 𝑦))/𝑑𝑥 = 0 Calculating Derivative of sin2 𝑥 & cos^2 𝑦 sepretaly Finding Derivative of 𝒔𝒊𝒏𝟐 𝒙 (𝑑 (sin2Differentiate both sides of the equation d dx (y) = d dx ( x 1 x 2) d d x ( y) = d d x ( x 1 x 2) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




If Y X X 1 X 2 Find Dy Dx
views around the world You can reuse this answer Creative Commons License If x = cos t (3 2cos^2 t) and y = sin t (3 2sin^2 t), find dy/dx at t = pi/4 asked in Mathematics by Samantha ( 3k points) continuity and differntiability Misc 13 Find 𝑑𝑦/𝑑𝑥 , if 𝑦=〖𝑠𝑖𝑛〗^(−𝟏) 𝑥〖𝑠𝑖𝑛〗^(−1) √(1−𝑥2), – 1 ≤ 𝑥 ≤ 1 𝑦=〖𝑠𝑖𝑛〗^(−




Implicit Differentiation Find Dy Dx If Y 2 3xy X 2 7 Chegg Com




If Y Sqrt X 1 Sqrt X Then Dy Dx At X 1 Is Equal To Youtube
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreVerify that x^2 cy^2 = 1 is an implicit solution to \frac {dy} {dx} = \frac {xy} {x^2 1} If you're assuming the solution is defined and differentiable for x=0, then one necessarily has y (0)=0 In this case, one can easily identify two trivial solutions, y=x and y=x If you're assuming the solution is defined and The nice thing about this differential equation is that the dy dx is already isolated, therefore the answer can be obtained by simply integrating both sides ∫dy = ∫3x 2 x2 dx y = 3 2x2 −2x−1 C y = 3 2x2 − 2 x C 2 = 3 2 (1)2 − 2 1 C 4 − 3 2 = C 5 2 = C




How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic



Find Dy Dx When X 1 T 2 1 T 2 And Y 2t 1 T 2 Sarthaks Econnect Largest Online Education Community
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreImage transcriptions From question given y= ely, we have to find the differential dy whenox = 2 andlax = 04 long (b) when * = 2 and dx = 005 0 since dy = leyda Now put x= 2 and dx= 04 in equation to findvalue ofdy we get, 16 dy Ley ( 0Calculus Find dy/dx y=x^2e^x y = x2ex y = x 2 e x Differentiate both sides of the equation d dx (y) = d dx (x2ex) d d x ( y) = d d x ( x 2 e x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps



Http Abacus Bates Edu Etowne towne105reviewsoln Pdf




Differentiation The Derivative And The Tangent Line Problem Ppt Download
5) d dx x x x () 10 10 1 g32 g16 6) If y = log x then dy dx = 1 x 7) If y = e 2 then dy dx = 2e 8) The derivative of a x is a xloga 9) The derivative of x m y n = (xy) (mn) is x y QIV Solve the following 1) If y = (6 x 3 − 3 x 2 −9 x) 10, find dy dx 2) If y = 3 8 5 2 4 5 x x g14 g14 g11 g12, find dy dx 3) If y = log(log(logx)) 2Find $ \dfrac{dy}{dx} $ if $ y = 2u^2 3u $ and $ u = 4x 1 $ I am trying to use the chain rule on it $$ \dfrac{dy}{dx} = \dfrac{dy}{du} \dfrac{du}{dx} $$ My work so far $$ \dfrac{d}{du}(2u^23u) * \dfrac{d}{dx}(4x1) = (4u3)(4) $$ However I am not absolutely sure I am doing it right and I don't have the answer in my bookFind dy/dx y= (x^2)/ (3x1) y = x2 3x − 1 y = x 2 3 x 1 Differentiate both sides of the equation d dx (y) = d dx ( x2 3x−1) d d x ( y) = d d x ( x 2 3 x 1) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps



Find Frac Dy Dx If Y Sin 1 X Sqrt 1 X Sqrt X Sqrt 1 X 2 0 X 1 Mathematics Stack Exchange



Find Dy Dx If Y Tan 1 A X 1 Ax Wyzant Ask An Expert
Q Please copy and paste the graphs into this file and provide a brief explanation of each You will receive points off if you simply copy and paste the outputs without a description 3) Creating a Dataset and Examining Basic Descriptive Statistics We will use the fictional data in the table below (see next page) Transcript Ex 53, 9 Find 𝑑𝑦/𝑑𝑥 in, y = sin^(−1) (2𝑥/( 1 2𝑥2 )) 𝑦 = sin^(−1) (2𝑥/( 1 2𝑥2 )) Putting x = tan θ 𝑦 = sin^(−1"Find "(dy)/(dx)" for "y=sin(x^(2)1) Updated On To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!




Ex 5 3 10 Find Dy Dx In Y Tan 1 3x X3 1 3x2 Ex 5 3



Web Northeastern Edu Dummit Teaching Fa19 1341 1341 Midterm 1 Review Problems Pdf
Y 1 d y = x − 1 d x Variable x cannot be equal to 1 since division by zero is not defined Multiply both sides of the equation by \left (x1\right)\left (y1\right), the least common multiple of y1,x1 Variable x cannot be equal to 1 since division by zero is not defined Given that dy/dx = 9y²– 4 and that y = 1 when x = 2 Find an equation expressing x in term of y Example 9 Find the general solution of the differential equation 𝑑𝑦/𝑑𝑥= (𝑥1)/ (2−𝑦) , (𝑦≠2) 𝑑𝑦/𝑑𝑥= (𝑥 1)/ (2 − 𝑦) , (𝑦≠2) (2 − y) dy = (x 1) dx Integrating both sides ∫1 〖 (2−𝑦)𝑑𝑦=〗 ∫1 (𝑥1)𝑑𝑥 2y − 𝑦^2/2 = 𝑥^2/2 x c 〖4𝑦 − 𝑦〗^2/2 = (𝑥




Find Dy Dx If Y Tan Inverse Square Root Of 1 X 2 Square Root Of 1 X 2 Square Root Of Maths Continuity And Differentiability Meritnation Com




Misc 13 Find Dy Dx If Y Sin 1 X Sin 1 Root 1 X2 Miscellaneous
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If y= 1/x then dy/dx is Ex 53, 11 Find 𝑑𝑦/𝑑𝑥 in, 𝑦 = cos–1 ((1− 𝑥^2)/( 1 𝑥2 )) , 0 < x < 1 𝑦 = cos–1 ((1− 𝑥^2)/( 1 𝑥2 )) Putting x = tan θ yFind dy/dx y^2=(x1)/(x1) Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set as




Ex 5 3 14 Find Dy Dx In Y Sin 1 2x Root 1 X2 Cbse
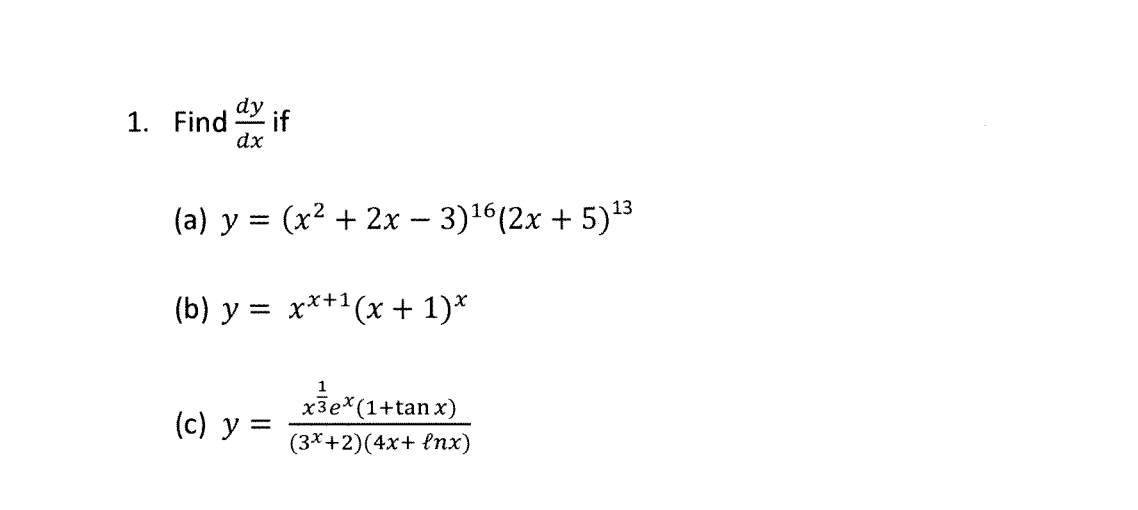



Find Dy Dx If Y X 2 2x 3 16 2x 5 13 Y Chegg Com
The derivative of the function `y = log(x 1/x)` with respect to x, `dy/dx` has to be determined It is assumed that log in the problem refers to natural logarithm




Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If




Find Dy Dx If Y U4 U 1 V V 5x2 2x 6 Maths Continuity And Differentiability Meritnation Com




Find Dy Dx Y X 2 1 3 2x 1 Sqrt X 3 4x 1




If Y Root Of 1 X 1 X Then Prove That 1 X 2 Dy Dx Y 0 Brainly In




If Y 3 U 2 U And U 4x 1 X 2 Find Dy Dx Brainly In




If Y X 1 Y Prove That X 2 Y 2 3 Dy Dx 1



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf



If Y X Sin X Cos X X 2 1 X 2 1 Find Dy Dx Sarthaks Econnect Largest Online Education Community




Eyzqfgnna2tanm




If Y Xx Prove That D2y Dx2 1 Y Dy Dx 2 Y X 0 Explain In Great Detail Mathematics Topperlearning Com X4m0m1ww




Find Dy Dx If Xy 2 Xy 2 E Y 3x X 3 Find The Chegg Com




If Y 1 X 2 X 1 Y 2 1 Prove That Dydx 1 Y 21 X 2




If Y Tan 1 X 1 Sqrt 1 X 2 Then Find Dy Dx




If Y X 1 X 1 X 5 Then Dy Dx Youtube




Find Dy Dx Y X X 1 X Brainly In




Chapter Differentiation Questions 1 Find The Value Of Answers 1 2 If F X 2 2x 5 Find F 2 Answers 2 3 If Y 2s And X 2s 1 Ppt Download




Find Dy Dx If Y Sin 3 X 2 I E Y Chegg Com




Chapter Differentiation Questions 1 Find The Value Of Answers 1 2 If F X 2 2x 5 Find F 2 Answers 2 3 If Y 2s And X 2s 1 Ppt Download




If Y 1 X 1 X 2 2 X 3 3 Then Dy Dx A




If Y 1 Sqrt A 2 X 2 Find Dy Dx



How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora
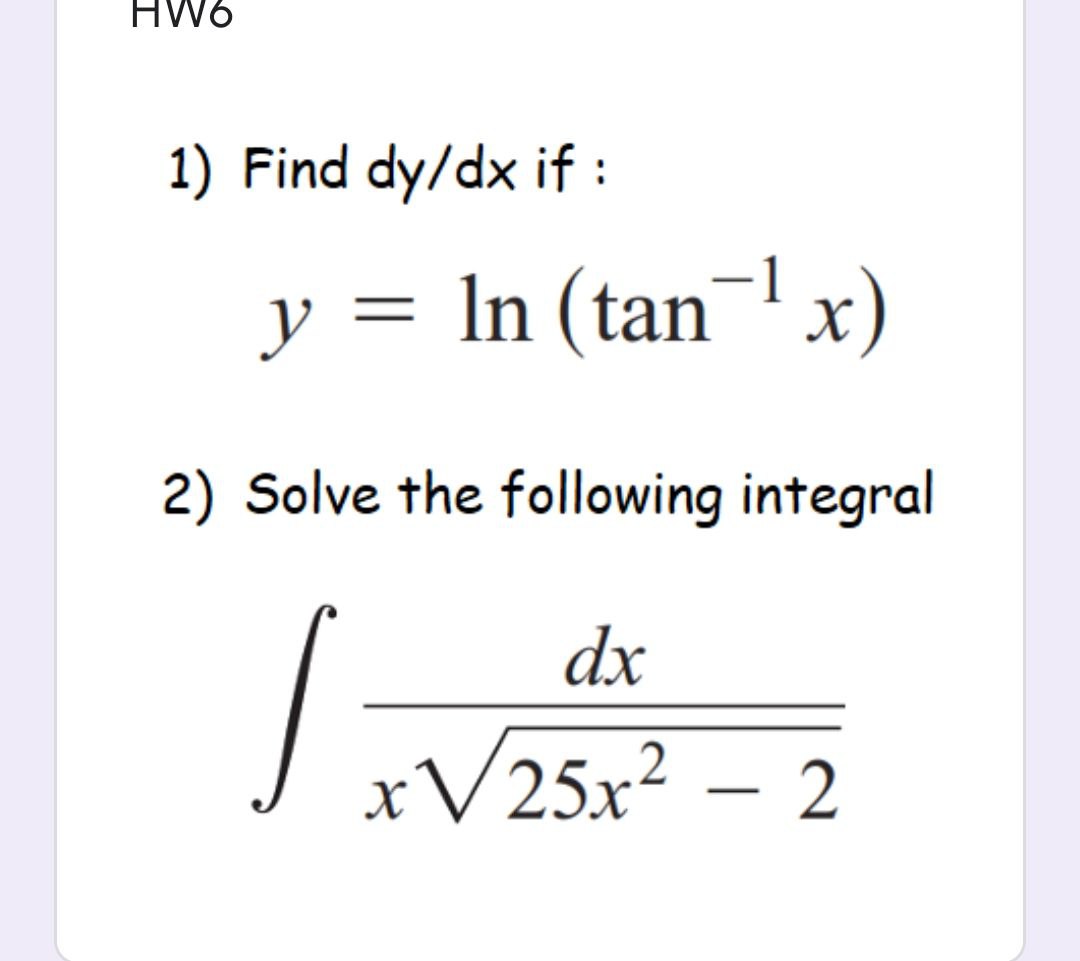



Answered 1 Find Dy Dx If Y Ln Tan X 2 Bartleby




If Y X X 1 X 2 Find Dy Dx




If Y X What Is Dy Dx Quora



How To Find Dy Dx When Y Cos 3cos X 4sinx 5 Quora




If Y 3x 2 2x Then Find Dy Dx Youtube




If Y 1 X 1 X 2 1 X 4 1 X 8 1 X 2n Find Dy Dx




Worked Example Differentiating Related Functions Video Khan Academy




2 Find Dy Dx If Y 3 Ind The First Derivative Of Chegg Com




Ex 5 3 11 Find Dy Dx In Y Cos 1 1 X2 1 X2 Ex 5 3




Find Dy Dx For Y Sin 1 2xsqrt 1 X 2 1 Sqrt2 X 1 Sqrt2 Mathematics Shaalaa Com




Find Dy Dx For The Given Function Y X 1 X 2 X Brainly In



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau
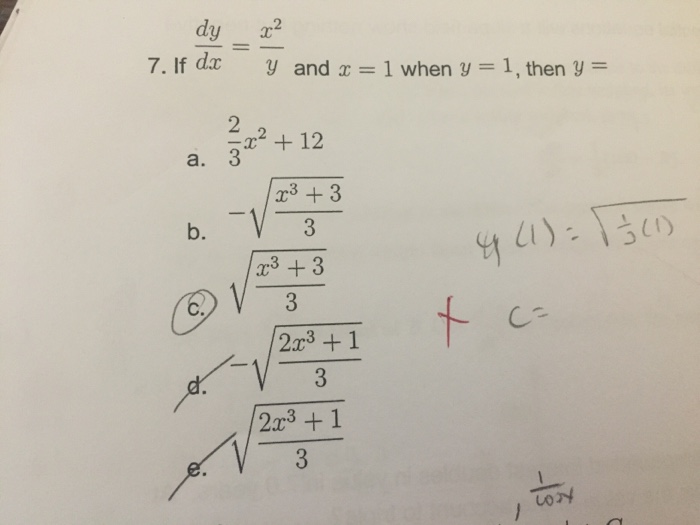



If Dy Dx X 2 Y And X 1 When Y 1 Then Y 2 3 Chegg Com




If Y X 1 X Show That 2x Dydx Y 2 X



What Is The Derivative Of X Xy Y 1 Quora




If X 1 Y 2 Y 1 X 2 1 Prove That Dydx 1 Y 2 1 X 2



Www Math Colostate Edu Clayton Teaching M113f10 Homework Hw7solutions Pdf



If Y X 2 1 Log 1 X 1 1 X 2 Find Dy Dx Sarthaks Econnect Largest Online Education Community



Find A Derivative With Step By Step Math Problem Solver




Iit 19 Find Dy Dx If Y F 2x 1 Square X 1 And F X Sin Square X Youtube




Find Dy Dx If Y X 1 X 2




Find Dy Dx If Y Frac X 13x2ln X Gauthmath




3 12 Find Dy Dx By Implicit Differentiation 9 4 Cos Chegg Com




Ex 5 5 12 Find Dy Dx Xy Yx 1 Class 12 Cbse Ncert




Find Dy Dx X 1 When Y 1 X X 9 X 10 X 5 Chegg Com
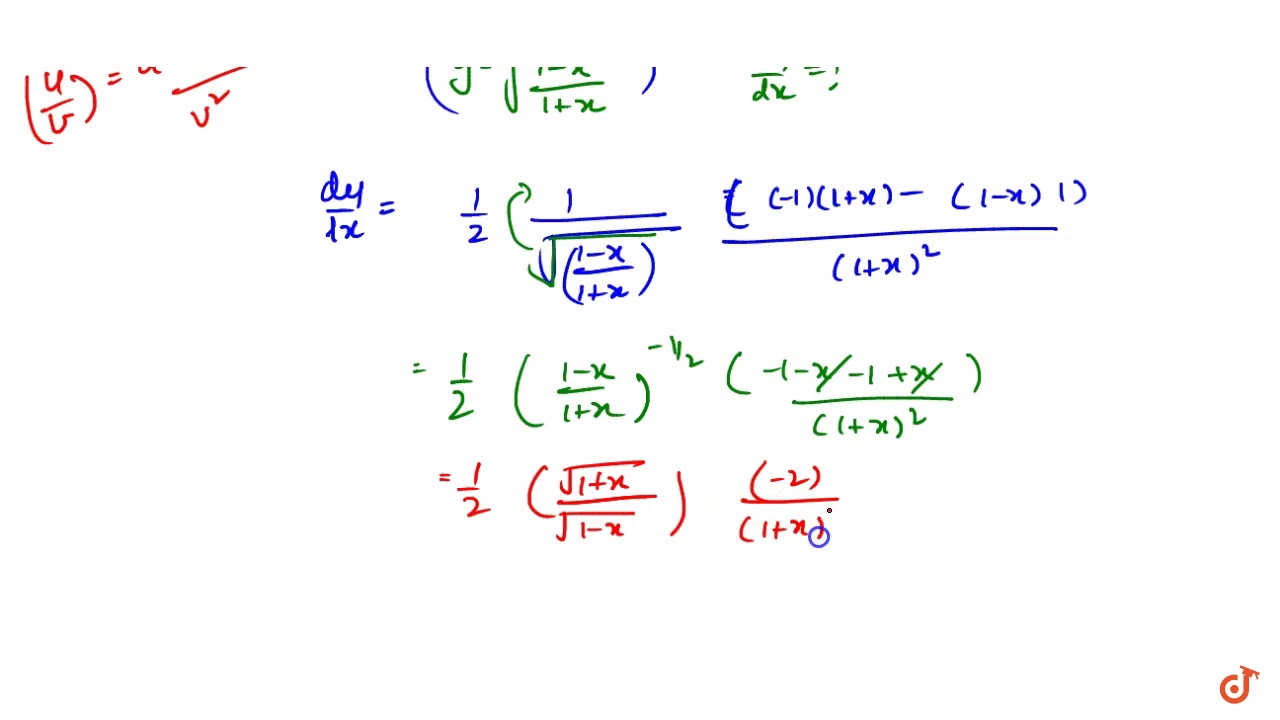



If Y Sqrt 1 X 1 X Then Dy Dx Equals Youtube




Find Dy Dx If Y 3 U 2 U Where U 4x 1 X2 Brainly In



If Y F 2x 1 X 2 1 And F X Sinx 2 Can You Find Dy Dx Quora




If Y X X 2 Then Dy Dx At X 1




Find Dy Dx If Y X 2 1 X 2 1 Brainly In




Lemh105



1



Q Tbn And9gcq9arl5ab K Kkztqdma6czzlslnfprp6ljv7o6a18 5qqda4yy Usqp Cau



2
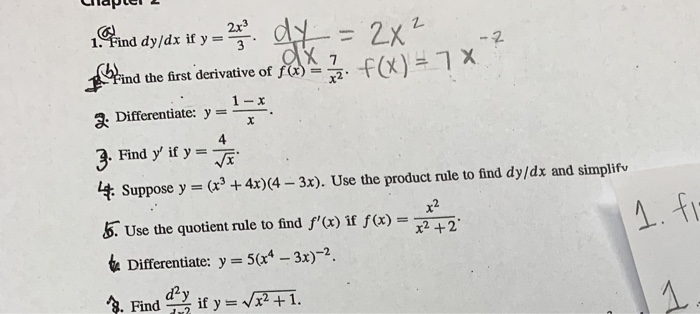



2 Find Dy Dx If Y 3 Ind The First Derivative Of Chegg Com




If Y X 1 X 1 Then What Is Dy Dx Equal To




If Y X X2 1 1 2 M Then Show That X2 1 D2y Dx2 X Dy Dx M2y 0 Mathematics Topperlearning Com 6jd9kell



How To Find Dy Dx When Y Sin X 2 Y 2 Quora
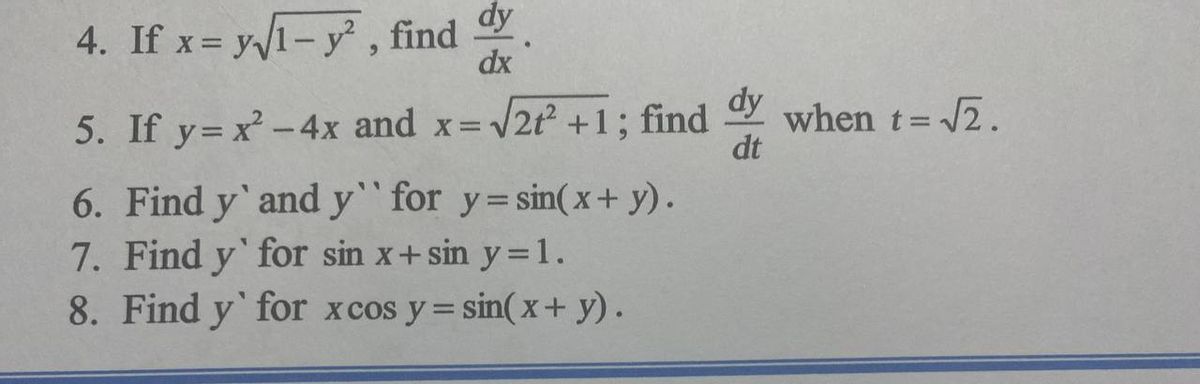



Answered 4 If X Y 1 Y Find Dy Dx 5 If Y Bartleby



1



How To Get The Special Solution Of This Differential Equation Y Xdy Dx 2 1 X 2 Dy Dx Where X 1 Y 1 Quora



Http Media Collegeboard Com Digitalservices Pdf Ap Ap16 Calculus Q4 Pdf




Find Dy Dx If Y Sin 1 X Sin 1 Sqrt 1 X 2 0 X 1 Mathematics Shaalaa Com




If Y 1 X Then Dy Dx Is Youtube




Ex 5 3 9 Find Dy Dx In Y Sin 1 2x 1 2x2 Chapter 5




If Y X X 1 X 2 Then Dy Dx Is Brainly In
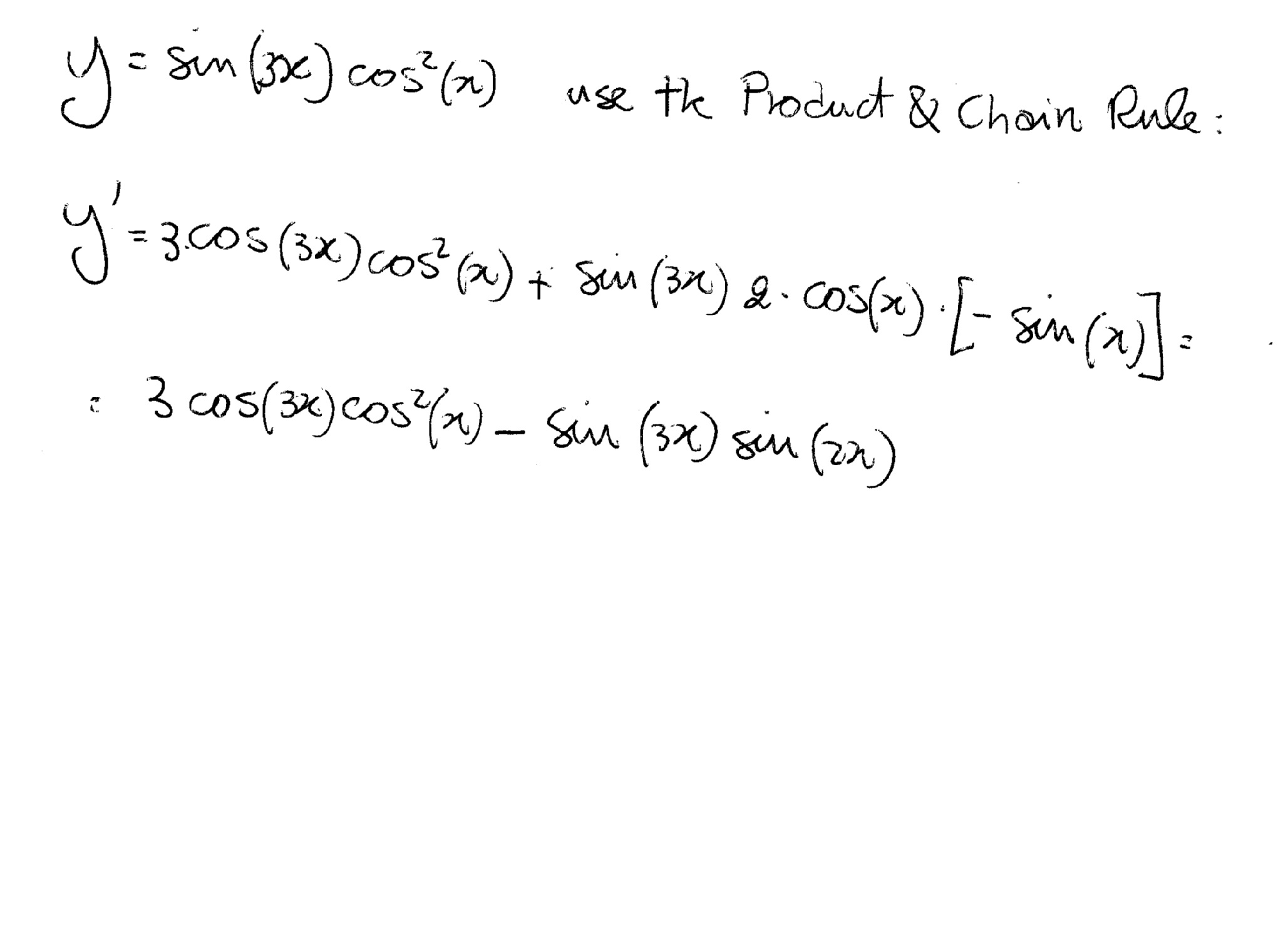



How Do You Find Dy Dx If Y Sin3x Cos 2 X Socratic




Chapter Differentiation Questions 1 Find The Value Of Answers 1 2 If F X 2 2x 5 Find F 2 Answers 2 3 If Y 2s And X 2s 1 Ppt Download
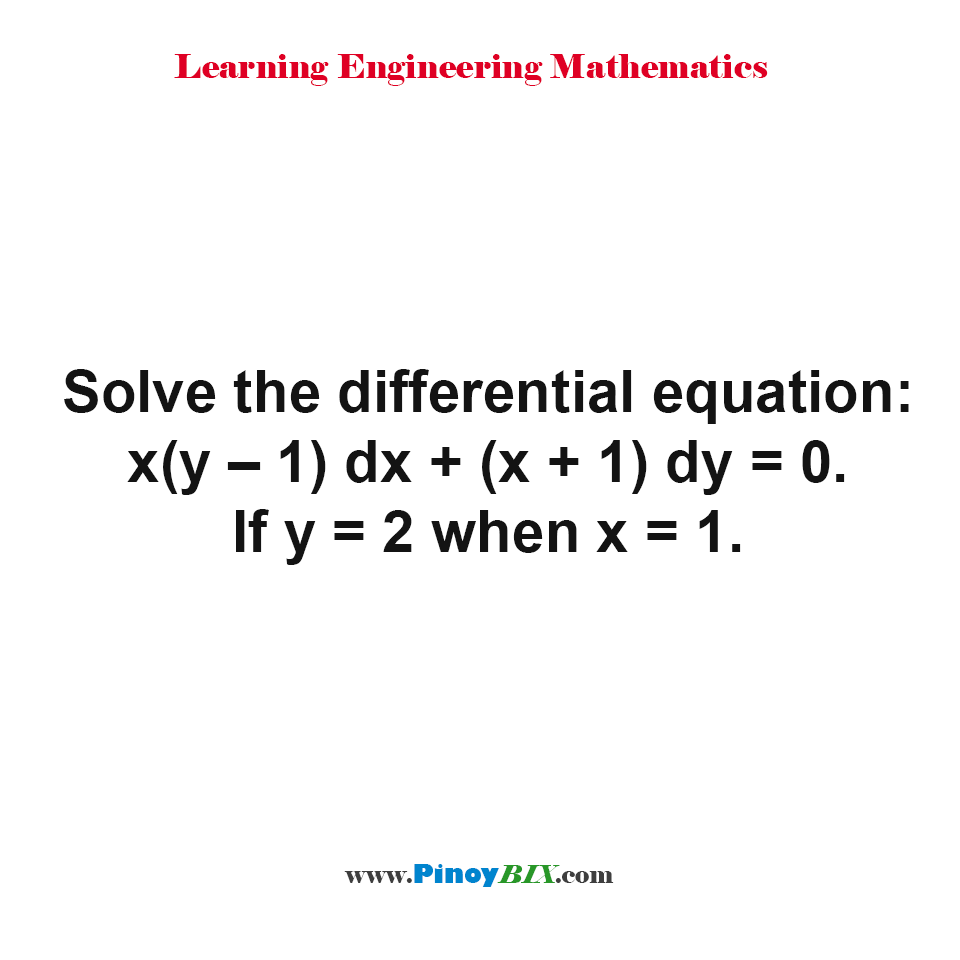



Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If Y 2 When X 1




Iit 1980 Find Dy Dx If Y 5 3 Sqrt Square 1 X Squarecos 2x 1 Youtube




Solve X X 1 Dy Dx Y X2 X 1 2 Maths Differential Equations Meritnation Com



Find Dy Dx If Y Xtanx X2 1 2 Studyrankersonline



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf



If Y X Is A Solution Of 2 Sinx 1 Y Dy Dx Cosx And Y 0 1 Then Find The Value Of Y P 2 Studyrankersonline




Find Dy Dx If Y Cos X X Sin X 1 X Brainly In
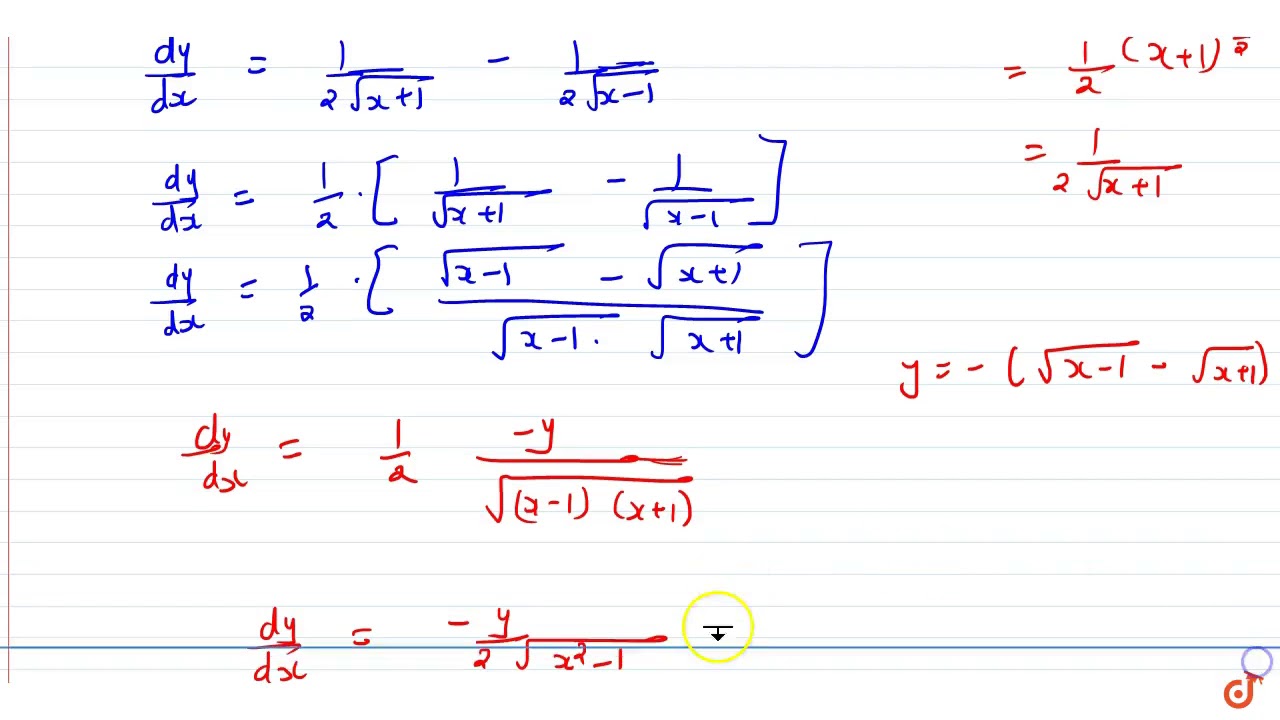



If Y Sqrt X 1 Sqrt X 1 Prove That X 2 1 D 2y Dx 2 X Dy Dx Y 4 0 Youtube




If Y Xcot X 2x2 3 X2 X 2 Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Palrsebb




If Y 1 X 1 X 2 I X 4 1 X 2n Then Find Dy Dx At X 0 Different Class 12 Maths Differentation Ramadan




If Y 1 X 1 X 2 1 X 4 1 X 2n Then The Value Of At X 0 Is




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12




Solution Find Dy Dx At The Point 0 1 If Y 5 X 2 4 E Xln Y Amp 8722 15 Amy



0 件のコメント:
コメントを投稿